終於到了尾聲，本書的最後 80 頁我看了 2 次，不太確定自己到底有沒有讀錯，總之就來努力摘要一下。

終盤的主題是：

• 具體化
• 逆向思考
• 培養數學的美感 - 合理性、對稱性、一致性（結語）

過程中穿插各種高中數學與意想天開的舉例，最後的總結是：

• 數學是一門建立在「看穿事物本質」之精神上的學問。
• 但尚未被揭發的本質究竟躲在哪裡呢？⋯⋯遍尋不著時，大部分的人都會不自覺地往複雜的方向思考。在這種時候，不妨讓思緒回到最單純的狀態。
• 當你認為自己發現了「本質」，但想確認它是不是真正的本質時，請檢視該本質是否可以用來統一說明大部分的情況。如果它只適用於特定情況，那肯定不是真正的本質。
• 想要統一說明、甚至想讓說明愈簡單愈好的欲望，就是一種「非常數學」的思維。這樣的思維正是帶領我們看穿事物本質的最佳功臣。

具體化

要把一件事說清楚，需要「往返在具體與抽象之間」。

• 整理、順序、轉換、抽象化等前半局的主題，目標是「提升說明能力」
• 後半的目標是：「以邏輯性的方式進行推論」

透過邏輯性的方式，由己知情況推導出未知的兩種方法：

• 演繹法：
  • 從適用全體的理論（假說），推導至個別狀況
  • 缺點：假說有誤、或套用範圍受限時，就可能會把假說套用在不適合的情況
• 歸納法：
  • 從個別狀況推導出適用全體的理論
  • （也就是從多組具體實例中找出共通性質，再加以抽象化）
  • 缺點：無法驗證所有事例，或提出同等邏輯證明時，最後的抽象結論未必為真，要注意有機率的要素。

舉例說明：

• 用一元二次方程式的解題過程舉例，直接套公式是演繹法，而從個案推導公式是歸納法。
• 在開發產品的「調查-企劃-設計-試做-推銷」流程中，交替使用演繹/歸納，可發揮極大的力量。

逆向思考

數學的舉例：

• 求「圖形面積」時，可以從全體扣除特定圖形，得到剩餘面積。
• 機率型題目中，問幾種情況。例如「投擲 4 枚硬幣，至少有 1 枚是正面的機率是多少」
  • 此時要逐一考量時的計算比較麻煩
  • 而逆向思考可以從「全部為反面」的情況來計算，也就是差集的思考，算式為 1-[(1/2)^4] = 15/16

神奇的舉例 - 分析造成情緒的事件 - ABC 理論

• 發生了某事件（A），就會產生情緒結果（C）
• A 到 C 之間有 Belief 的運作，而 B 段又有理性/非理性的類型
• 當 B 段為非理性思考時，要從中跳脫，需要進入第四段 Dispute，進行逆向思考，才能找回思考的彈性

在神奇的心理學案例後，進入了「逆向」的邏輯證明 XD

• 「若 P 則 Q」的逆向有可能是⋯⋯
  • 若 Q 則 P （逆命題）- 前後互相對調
  • 非 P 則非 Q（否命題）- 前後不變，但分別改成否定
  • 非 Q 則非 P（對偶命題）- 前後互相對調，且分別改成否定
• 白話文對照「如果努力沒有回報 (P)，就不算是真正的努力 (Q)」
  • 若 Q 則 P （逆命題）- 若不是真正的努力 (Q)，就不會得到回報 (P)
  • 非 P 則非 Q（否命題）- 如果努力得到了回報 (P')，就算是真正的努力 (Q')
  • 非 Q 則非 P（對偶命題）- 如果是真正的努力 (Q')，就一定會得到回報 (P')
• 按照定義整理：

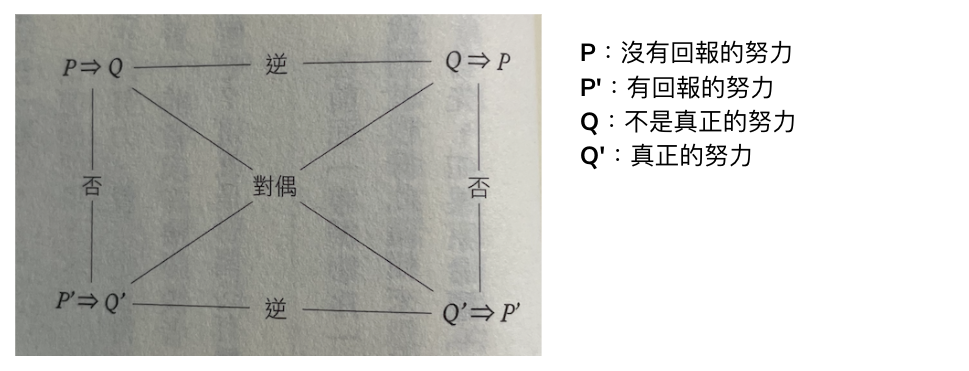
由於原命題和對偶命題的真偽完全一致（互為充要），因此最適合拿來進行逆向思考。（然後作者又畫了一次圖形來確定關係是「小→大」）

逆向思考的意義是，當原始命題難以判別真偽時（例如受到情緒影響時），可以改用對偶命題來思考。（接著展示了高中數學證明題⋯⋯）

本節最後還介紹了⋯

• 反證
  • 先假設某命題不成立
  • 導出矛盾結果
• 二律背反：
  • 互相矛盾的兩個命題同時成立
  • 例如「他是加害者也同時是受害者」
• 當二律背反成立時，反證明就毫無用武之地，此時需要深入思考，因此進行邏輯思考時，需要具備辨識二律背反的能力。

數學的美感

由於已經到終章了，所以介紹幾個大原則：

• 合理性 - 總之就是用自己的頭腦思考，培養出一顆能感受合理之美的心
• 對稱性 - 活用美感，產生對稱，例如「數」和「圖形」的關聯
• 一致性 - 美麗的公式與真理們

在說明「對稱性」的時候，作者用座標計算來說明。

然後最後用一個 Google 面試題，鼓勵大家要保持挑戰奇怪問題的好奇心。

END

其實本來想偷懶快速筆記的，但總覺得太省略會讓論述看起來很荒謬（啊是我那顆感受合理之美的心嗎），只好在連假的尾聲認真地做了筆記。

話說，因為我一直念念不忘中文書名「喚醒你與生俱來的數學力」，在閱讀過程中，我一直好奇「到底在【喚醒】什麼【數學力】呢？」本書下半場進入邏輯世界後，我對於「喚醒」那兩個字實在耿耿於懷。

最後覺得可能是翻譯書名太浮誇了，重新查了原文書名「根っからの文系のためのシンプル数学発想術」，不太確定日文的斷句邏輯，但應該比較像是「從文組角度而寫的簡單數學思考術」。

就說嘛！！！哪有「喚醒」那麼浮誇！！！！

嗯總之我的數學力應該還沉睡在地底三千呎，還沒醒來謝謝。不過這本書很好看，各位如果有什麼剛上高中的堂表弟妹們，可以考慮送這本書當成禮物。